Can’t figure out how to do this without equations, sorry in advance for any heads that may explode in trying to read this post. Converting viscosity change to drag change sounds like it should be pretty easy but it isn’t. Shear force at the wall (foil surface) has a pretty short formulation of

And suggests at first glance that shesr force is directly proportional to viscosity. But viscosity changes also change the other part of that equation, the velocity profile in the boundary layer as you move away from the wall perpendicularly. So, you get some simplified approximations, for a flat plates anyways.
For laminar flow
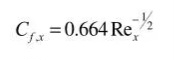
And for turbluent flow over a relevant Reynolds number range (I estimate the same values as you @seawing)
![]()
What does this mean? Last equation, promise

Putting it all together, skin friction is proptional to the square root of viscosity in laminar flows and the 5th root of viscosity in turbulent boundary layer flows. This means for a 50% increase in viscosity, skin friction increases by 22% in laminar flows and 8.4% in turbulent boundary layers flows.
So then the question is, how much of the flow over our foils is laminar and how much is turbulent? Boundary layers always start out laminar and then, at a high enough local Reynolds (take distance from the leading edge as length) number trip to turbulent. Exactly where this trips depends on Reynolds number (speed, viscosity, density, and distance from leading edge along chord), surface roughness, initial level of turbulence in the water (white wash, strong currents, etc) and contaminants like silt or oil. But in general, at low speed and especially for a light rider that can go slow on a small foil, flow over the foil may be entirely laminar. While at high speed the flow could be almost entirely turbulent, especially in a turbulent or silty chunk of water.
So up to 22% more skin friction at low speed and as low as 8% more at high speed if viscosity goes up by 50%.
But, have to remember skin friction isn’t the only cause of drag. Also have profile (pressure) drag and induced drag and their contributions will dilute the effect of viscosity changes. The relative significance changes with speed, for a given rider weight. At low speed/high angle of attack, pressure and induced drag dominate. At high speed/low angle of attack, skin friction dominates.
So, how much do viscosity changes matter at the end of the day? It very much depends, unfortunately. But given that many foilers notice (lose their mind over?) a few percent change in weight, I would say it is at least noticeable in all circumstances where the viscosity change is large, 25% or more say, and very significant in situations where skin friction is the dominant drag component.
If you are still reading at this point, cheers and I hope your head is intact.