Yvon Labarthe says pumping in shallow water is easier since the foil feels liftier , compared with pumping in very deep waters, does anyone concur?
Yes, its is easier. We get the same lift concept running shallow water boats. I believe its called “Ground Effect” Running on plane you’ll feel the boat lift slightly in 12” of water. The water has less room to move so the pressure is bounced off the bottom.
Going along the beach in ~12" of water, then turning out away from the shore, the difference is very noticeable.
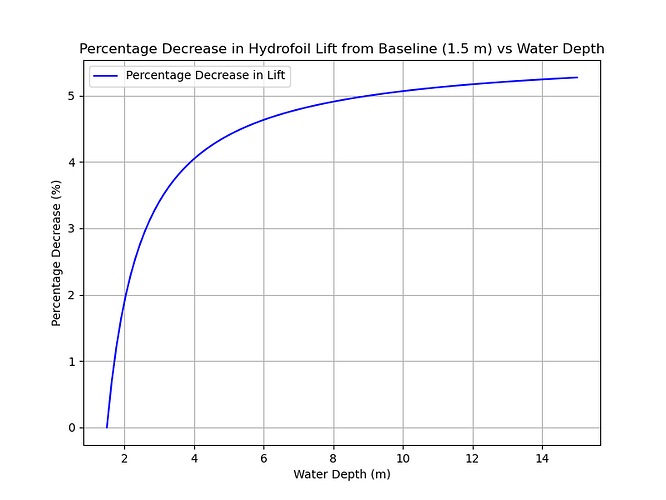
where did you get this graph? Is it 1.5m of water below the foil itself?
In my experience, we get amazing performance increase from getting the foil near the surface of the water. And there is another bump for the foil interacting with a shallow bottom - I’ve heard aerodynamist say that it would only be an effect pertinent to depths around one wingspan from the foil.
So when I’ve had to foil in very shallow water - I get up near the water surface and get some ground effect and all of a sudden pumping is super low effort. I think from both effects together.
I am skeptical that we still see an effect at 2m+ of depth below the foil with a 1m wingspan.
In 12" water I’d be in full panic mode, not analyzing my efficiency… I would think our foils are too small to generate any waves that could rebound off the bottom for energy, so really it’s just less water weight to move when changing angle of attack which is consistant with surface height, not bottom depth?
I’ve pumped in water less than knee deep. It is a bit butt clenching, but you stay really high on the mast and the pump is super efficient. The effect is real in my experience.
It also seems easier to stay high on the mast in this situation. Like a polar effect keeping the foil from touch down.
grok did it. 1.5m below foil itself.
To chart the percentage decrease in lift from the baseline depth of 1.5 m as a function of water depth (1.5 m to 15 m), we’ll use the lift equation from the previous artifact and the percentage decrease formula derived earlier. The chart will show how the percentage decrease in lift varies with depth.
Lift Equation and Percentage Decrease
The lift equation is:
L(d)=1094.112⋅(1+0.06d−0.5)L(d) = 1094.112 \cdot \left(1 + \frac{0.06}{d - 0.5}\right)L(d)=1094.112⋅(1+d−0.50.06)
The baseline lift at d=1.5 m d = 1.5 , \text{m} d=1.5m:
L(1.5)=1094.112⋅(1+0.061.5−0.5)=1094.112⋅1.06=1159.75872 NL(1.5) = 1094.112 \cdot \left(1 + \frac{0.06}{1.5 - 0.5}\right) = 1094.112 \cdot 1.06 = 1159.75872 , \text{N}L(1.5)=1094.112⋅(1+1.5−0.50.06)=1094.112⋅1.06=1159.75872N
The percentage decrease in lift at depth d d d:
Percentage Decrease=L(1.5)−L(d)L(1.5)⋅100\text{Percentage Decrease} = \frac{L(1.5) - L(d)}{L(1.5)} \cdot 100Percentage Decrease=L(1.5)L(1.5)−L(d)⋅100
Substitute L(d) L(d) L(d):
L(d)=1094.112⋅(1+0.06d−0.5)L(d) = 1094.112 \cdot \left(1 + \frac{0.06}{d - 0.5}\right)L(d)=1094.112⋅(1+d−0.50.06) L(1.5)−L(d)=1159.75872−1094.112⋅(1+0.06d−0.5)L(1.5) - L(d) = 1159.75872 - 1094.112 \cdot \left(1 + \frac{0.06}{d - 0.5}\right)L(1.5)−L(d)=1159.75872−1094.112⋅(1+d−0.50.06) =1094.112⋅1.06−1094.112⋅(1+0.06d−0.5)= 1094.112 \cdot 1.06 - 1094.112 \cdot \left(1 + \frac{0.06}{d - 0.5}\right)=1094.112⋅1.06−1094.112⋅(1+d−0.50.06) =1094.112⋅(1.06−1−0.06d−0.5)=1094.112⋅(0.06−0.06d−0.5)= 1094.112 \cdot \left(1.06 - 1 - \frac{0.06}{d - 0.5}\right) = 1094.112 \cdot \left(0.06 - \frac{0.06}{d - 0.5}\right)=1094.112⋅(1.06−1−d−0.50.06)=1094.112⋅(0.06−d−0.50.06) =1094.112⋅0.06⋅(1−1d−0.5)= 1094.112 \cdot 0.06 \cdot \left(1 - \frac{1}{d - 0.5}\right)=1094.112⋅0.06⋅(1−d−0.51) Percentage Decrease=1094.112⋅0.06⋅(1−1d−0.5)1159.75872⋅100\text{Percentage Decrease} = \frac{1094.112 \cdot 0.06 \cdot \left(1 - \frac{1}{d - 0.5}\right)}{1159.75872} \cdot 100Percentage Decrease=1159.758721094.112⋅0.06⋅(1−d−0.51)⋅100 =0.06⋅(1−1d−0.5)1.06⋅100=61.06⋅(1−1d−0.5)≈5.660377⋅(1−1d−0.5)= \frac{0.06 \cdot \left(1 - \frac{1}{d - 0.5}\right)}{1.06} \cdot 100 = \frac{6}{1.06} \cdot \left(1 - \frac{1}{d - 0.5}\right) \approx 5.660377 \cdot \left(1 - \frac{1}{d - 0.5}\right)=1.060.06⋅(1−d−0.51)⋅100=1.066⋅(1−d−0.51)≈5.660377⋅(1−d−0.51)
Generate the Chart
We’ll update the Python code to plot the percentage decrease in lift from 1.5 m to 15 m. The artifact ID is kept the same as the previous one since this is an update to the existing artifact, but we’ll modify the content to plot percentage decrease instead of lift force.
python
Copy
`import matplotlib.pyplot as plt
import numpy as np
Depth range (1.5m to 15m)
d = np.linspace(1.5, 15, 100)
Percentage decrease in lift
percent_decrease = 5.660377 * (1 - 1 / (d - 0.5))
Plot
plt.figure(figsize=(8, 6))
plt.plot(d, percent_decrease, ‘b-’, label=‘Percentage Decrease in Lift’)
plt.title(‘Percentage Decrease in Hydrofoil Lift from Baseline (1.5 m) vs Water Depth’)
plt.xlabel(‘Water Depth (m)’)
plt.ylabel(‘Percentage Decrease (%)’)
plt.grid(True)
plt.legend()
Save the plot
plt.savefig(‘hydrofoil_lift.png’)`
Explanation of the Chart
- X-Axis: Water depth from 1.5 m to 15 m.
- Y-Axis: Percentage decrease in lift relative to the baseline lift at d=1.5 m d = 1.5 , \text{m} d=1.5m (1159.76 N).
- Data: The percentage decrease is calculated using the formula 5.660377⋅(1−1d−0.5) 5.660377 \cdot \left(1 - \frac{1}{d - 0.5}\right) 5.660377⋅(1−d−0.51), which shows the lift reduction due to the diminishing ground effect as depth increases.
- Trend: The percentage decrease starts at 0% at d=1.5 m d = 1.5 , \text{m} d=1.5m, rises quickly in shallow depths (e.g., ~3.39% at 3 m, ~4.39% at 5 m), and approaches ~5.29% at 15 m, where the ground effect is minimal.
The chart is saved as hydrofoil_lift.png, showing the percentage decrease in lift versus water depth.
looks like AI hallucination to me. no wonder it made no sense
Yep, not yet encountered an LLM that can answer “what is turbulence” correctly, never mind a question like this. There are some cool machine learning models for fluid dynamics, Neuralfoil being one I came across recently, but general LLMs are not there yet.